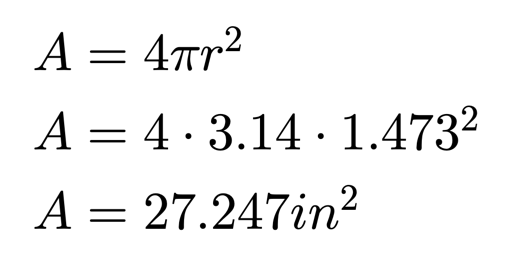Sphero's volume and surface area
Basic math to understand Sphero’s geometry
Sphero is a sphere with volume and surface area. To calculate these values, we need one piece of information. We need to know the radius.
The radius is the distance from the center of the sphere to any point on the surface. We know that a line drawn from one point on the surface through the center and to another point is the diameter. The radius is half the length of a diameter. This information is similar to that of a circle.
There isn't a way for us to measure the radius of our sphere. We would need to disassemble the robot. We can, however, measure around the sphere. There are two values that we can measure. Both of these values will help determine the information we need.
Let’s begin with the easiest. For this exercise we will need a length of string. The string should be at least twelve inches long. The string shouldn't be too thick.
Find the seam along Sphero’s surface. Place one end of the string on a point on the seam. Wrap the string around the seam until it meats up with the string’s starting point. Use a marker or pen. Mark where the string meats the starting point. This measurement isn’t very accurate but we will round our measurement later.
Use a ruler. Place the starting end of our string at the beginning of the ruler’s measurement. Lay the string along the ruler. Find where the point we marked the string lays on the ruler. This is the circumference.The circumference from the measurements of my Sphero resulted in approximately nine and a quarter inches, 9.25in. The equivalent measurement in centimeters is 23 cm. Most rulers have both units of measure.
To determine the radius we need to use the formula for the circumference of a circle. The formula multiplies the diameter by Pi. To solve for radius we need to reformat our formula. This step takes us into the use of algebra.
We want the diameter to be on one side of our equation. Let’s begin by writing down our values into the equation. Take the value of the measurement and write it down. Place an equal sign to the right and then the value of pi, 3.14. Place the multiplication symbol to the right of pi and D for diameter.
We need to move the value of pi to the left side of the equal sign. To do this we need to divide by pi. Place a divisor and the value of pi under the circumference. Place a divisor and the value of pi under pi.
When we divide a number by the same number the answer is always one. Pi divided by Pi is one. One times the diameter is the diameter. We don’t need to write the number one.
Dividing the circumference by pi gives us the diameter. The diameter in inches is approximately 2.945 inches. The diameter in centimeters is approximately 7.324 cm. The value we get here is an approximation. The diameter is twice the radius. To get the radius we divide the diameter by two. The radius in inches is 1.473 in. The radius in centimeters is 3.662 cm.
Rounding the values for radius would seam to be reasonable but we will stay with this to review operations with decimal values. With the radius of our sphere we have the information needed to solve for surface area and volume.
The surface area of a sphere is calculated by squaring the radius. The product is multiplied by pi. This product is then multiplied by four. We’ll use my measurement in inches first. The radius from my diameter of 2.945, is 1.473. This gives us an approximate surface area of 27.247. We must state the units of measure in the answer. The complete answer is 27.247 square inches.
The volume is calculated by cubing the radius. This value is multiplied by pi. That value is then multiplied by 4 and divided by 3. The volume is approximately 13.387 cubic inches.
Now we will calculate the surface area and volume using our measurement in centimeters. The radius from our diameter, 7.324 is approximately 3.662. The volume is approximately 205.704 cubic centimeters. The surface area is approximately 168.518 square centimeters.
Recalculate with rounding
The answers from our measurement of Sphero’s circumference are approximations. The string and ruler are not the most accurate tools. I used a Vernier caliper to measure Sphero’s diameter. A Vernier caliper is a ruler with a measurement scale. It is used to take precise measurements. With the caliper I measured Sphero’s diameter at 7 centimeters. Use this updated measurement to recalculate Sphero’s volume and surface area.
Here are my answers so you can compare. Sphero’s volume is 179.594 cubic centimeters. Round this to 180 cubic centimeters. The surface area is 153.938 square centimeters. Round the value to 154 square centimeters. I will use these values from this point forward.
The information we gathered in these math activities will be used in our science activities. Remember the values for volume because they will come up again later.
Blog banner image inspired by Freepik