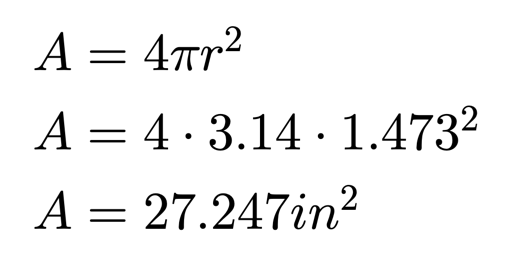Sphero's weight, mass, and density

The Science

Sphero is a physical object. It has mass and it has weight. We will use mass to determine buoyancy. Yes, Sphero floats.

Mass is the amount of matter an object has. The mass of an object remains the same or constant.

The weight of an object is the affect of gravity on an object. The weight depends on the gravity. The gravity on Earth is constant for our purposes. Gravity is affected by altitude on Earth. There is a close connection between mass and weight but they are two separate things.

Gravity relies on the mass of the Earth. It also relies on the elevation of the object weighed. Objects on the surface of the earth feel a greater pull by gravity. Objects in orbit around the earth, like a satellite, don’t feel the pull of gravity as much. This is why objects in space are said to be weightless.

An astronaut on earth could weigh about 200 pounds. In space that same astronaut’s weight can’t be measured. This is because there is not gravity to push down on the weight scale.

This is what makes mass different from weight. The astronaut has not changed. His or her matter has remained the same. Everything is made of matter. Some matter is light and some is heavy. The measurement of this amount of matter is called mass. The more matter something has the greater it’s mass.

Sphero’s Weight

There are a variety of ways to weigh Sphero. The easiest is to use a kitchen scale. Sphero comes with a base for charging. We will use this base to prevent it from rolling off the scale. Get yourself a kitchen scale. Turn on the kitchen scale and place the charging base on the scale. The scale will read the weight of the charging base.

We need to subtract this weight. There are a couple of ways to do this. The most obvious way is to take the base weight and subtract it from the total weight after adding the Sphero. Another way to eliminate the base weight is to use the Tare option on the scale. Most modern kitchen scales have this option. There is usually a button on the scale that reads Tare.

To use the Tare, press the Tare button on the scale. The scale will eliminate the base’s weight and display a zero. Just like the base was not on the scale.

Place Sphero on the base and read the weight on the scale. In Standard measurement, Sphero weighs approximately 6.35 ounces. In the Metric System, Sphero weighs 180 grams.

Sphero’s mass is 180 grams. The scale compensates for Earth’s gravity. Earth has a constant gravitational pull of 9.807 meters per second squared. The scale eliminates this force from our value.

A Balance scale

Let’s use a balance scale to check our value. Balance scales are used to measure mass. We use a balance scale to measure the mass of one object with the mass of another. We place one object on one side of the scale. On the other side we place objects that have a known mass. The objects are usually metal weights.

The mass of the weights is marked on each. We place enough of these weights until the scale is balanced. The total mass placed on the scale is used as a measure of the mass on the other side.

The the value of the weights placed on the other side of the balance total 180 grams. This agrees with the value from the kitchen scale.

This is part of the scientific process. We take measurements and then we need to verify those measurements. If the measurements are different then we need to understand why.

Buoyancy and Density

We know that Sphero floats. It is water tight. Make sure there are not cracks on your Sphero. These lessons cover buoyancy, density, and water displacement.The buoyancy of something depends on its density. Water has a density of 1. Objects that have a density greater than one will sink. Objects that have a density less than one will float. We will calculate the density of Sphero in a moment.

First, we need to know how we arrived at the density of water. Place a beaker on the kitchen scale. Press the Tare button to set the scale to zero. Pour 250 mL of water into the beaker. Read the measurement on the scale. Make sure the measurement units are in grams. The measurement is the same as the amount of milliliters we placed in the beaker.

To determine the density of water we divide the mass by the volume. The volume in milliliters is 250. The mass in grams is 250. The answer is one. The density of water is one.

Sphero’s Density

Sphero is enclosed in a plastic sphere. We will place Sphero into water and use it to learn about buoyancy and density. Buoyancy is the capacity for something to float. The density of an object has much to do with its ability to float.

We need a container with water. The container needs to have a way for us to measure the amount of water. A beaker is a good container to use if you have one large enough. I find that a two-cup kitchen measuring cup works well if a beaker isn't available. These measuring cups are available at any discount store for a few dollars. They have a nice handle to hold onto.

Fill the container to the one-cup measurement. Add some food coloring to help you see the water level if necessary.

Insert Sphero into the measuring cup. Sphero displaces the water in the measuring cup. Sphero forces the water up and around the measuring cup. The water level rises to one-and-three-quarter cups. Sphero displaces three-quarters of a cup of water.

Sphero doesn't completely float and it doesn't completely sink either. This is due to Sphero’s density.

To find the density of an object we need to divide the mass of the object by the volume. This is where all the math we did earlier comes together.

Sphero has a mass of 180 grams. It has a volume of 180 cubic centimeters. Sphero’s density is One! This is the same density as that of water. This explains why most of Sphero is submerged in water. Much like an iceberg.

All the science we just did would not be possible without the math we used in the previous lessons. This is that math science connection we are always wanting to make with students.

Sphero's volume and surface area

Basic math to understand Sphero’s geometry

Sphero is a sphere with volume and surface area. To calculate these values, we need one piece of information. We need to know the radius.

The radius is the distance from the center of the sphere to any point on the surface. We know that a line drawn from one point on the surface through the center and to another point is the diameter. The radius is half the length of a diameter. This information is similar to that of a circle.

There isn't a way for us to measure the radius of our sphere. We would need to disassemble the robot. We can, however, measure around the sphere. There are two values that we can measure. Both of these values will help determine the information we need.

Let’s begin with the easiest. For this exercise we will need a length of string. The string should be at least twelve inches long. The string shouldn't be too thick.

Find the seam along Sphero’s surface. Place one end of the string on a point on the seam. Wrap the string around the seam until it meats up with the string’s starting point. Use a marker or pen. Mark where the string meats the starting point. This measurement isn’t very accurate but we will round our measurement later.

Use a ruler. Place the starting end of our string at the beginning of the ruler’s measurement. Lay the string along the ruler. Find where the point we marked the string lays on the ruler. This is the circumference.The circumference from the measurements of my Sphero resulted in approximately nine and a quarter inches, 9.25in. The equivalent measurement in centimeters is 23 cm. Most rulers have both units of measure.

To determine the radius we need to use the formula for the circumference of a circle. The formula multiplies the diameter by Pi. To solve for radius we need to reformat our formula. This step takes us into the use of algebra.

We want the diameter to be on one side of our equation. Let’s begin by writing down our values into the equation. Take the value of the measurement and write it down. Place an equal sign to the right and then the value of pi, 3.14. Place the multiplication symbol to the right of pi and D for diameter.

We need to move the value of pi to the left side of the equal sign. To do this we need to divide by pi. Place a divisor and the value of pi under the circumference. Place a divisor and the value of pi under pi.

When we divide a number by the same number the answer is always one. Pi divided by Pi is one. One times the diameter is the diameter. We don’t need to write the number one.

Dividing the circumference by pi gives us the diameter. The diameter in inches is approximately 2.945 inches. The diameter in centimeters is approximately 7.324 cm. The value we get here is an approximation. The diameter is twice the radius. To get the radius we divide the diameter by two. The radius in inches is 1.473 in. The radius in centimeters is 3.662 cm.

Rounding the values for radius would seam to be reasonable but we will stay with this to review operations with decimal values. With the radius of our sphere we have the information needed to solve for surface area and volume.

The surface area of a sphere is calculated by squaring the radius. The product is multiplied by pi. This product is then multiplied by four. We’ll use my measurement in inches first. The radius from my diameter of 2.945, is 1.473. This gives us an approximate surface area of 27.247. We must state the units of measure in the answer. The complete answer is 27.247 square inches.

The volume is calculated by cubing the radius. This value is multiplied by pi. That value is then multiplied by 4 and divided by 3. The volume is approximately 13.387 cubic inches.

Now we will calculate the surface area and volume using our measurement in centimeters. The radius from our diameter, 7.324 is approximately 3.662. The volume is approximately 205.704 cubic centimeters. The surface area is approximately 168.518 square centimeters.

Recalculate with rounding

The answers from our measurement of Sphero’s circumference are approximations. The string and ruler are not the most accurate tools. I used a Vernier caliper to measure Sphero’s diameter. A Vernier caliper is a ruler with a measurement scale. It is used to take precise measurements. With the caliper I measured Sphero’s diameter at 7 centimeters. Use this updated measurement to recalculate Sphero’s volume and surface area.

Here are my answers so you can compare. Sphero’s volume is 179.594 cubic centimeters. Round this to 180 cubic centimeters. The surface area is 153.938 square centimeters. Round the value to 154 square centimeters. I will use these values from this point forward.

The information we gathered in these math activities will be used in our science activities. Remember the values for volume because they will come up again later.

Blog banner image inspired by Freepik